大後天是理查．費曼 (Richard Feynman, 11/5/1918 – 15/2/1988) 的 98 歲誕辰。他在 1964 年康奈爾大學 (Cornell University) 的著名演講 The Character of Physical Laws 裡，曾經說過：
It is scientific only to say what is more likely and what less likely, and not to be proving all the time the possible and impossible.
費曼是一位理論物理學家、1965 年諾貝爾物理學獎得主。雖然他的專業是抽象的理論物理，但他對科學的本質有深刻的見解。他說，科學並非去說什麼事情是可能或不可能。科學，是用理性與邏輯去分析事情的可能性。因為所有實驗、觀測，都必然有誤差和不確定性。
We have found it of paramount importance that in order to progress we must recognize our ignorance and leave room for doubt. Scientific knowledge is a body of statements of varying degrees of certainty – some most unsure, some nearly sure, but none absolutely certain.
我們幾乎可以說在這個宇宙之中，沒有任何事情是我們能夠百分百肯定的。我們必須要承認自己的無知、對事物心存懷疑。然而，我們不應該一味地說因知識所限，故所有的可能性都有同等地位。無知，並不代表我們對所有可能性都是同樣地不肯定。我們應該做的是不單止要把我們無知的部分考慮在內，更要把我們已知的部分同時考慮在內，這樣才是真正的客觀。
我來舉一個簡單的例子。我們有一個硬幣。我們可以問：這硬幣擲出來的正反面機率是多少？
想要知道答案，我們必須收集數據。如何收集？很簡單，拿這硬幣去擲，看看擲出正面和反面的頻率是否一樣就可以了。當然，在進行這個非常簡單的實驗之前，我們可以先猜一猜。正常情況下，如果我們沒有任何關於這硬幣的資訊，我們可能會猜測擲出正面的機率與擲出反面的機率相等，即是擲出正面的機率大概會是 50%，即 0.5，而且有一定的誤差。數學上這可以用一個峰值位於 0.5 的分佈表示。
或者，如果我們更加想表達對硬幣的資訊一無所知的話，我們也可以說擲出正面的機率介乎 0 (即是永遠不可能擲到正面) 到 1 (即是永遠不可能擲到反面) 之間，0 <= prob( head bias | I ) <= 1。我們不用太擔心這些符號和數字，這裡 head bias 代表得出正面的傾向、I 代表我們所知關於此硬幣的資訊、符號 | 是「在此情況下」的意思而已。如果 head bias 是 0.5 的話，就代表這個硬幣是公平的。如果 head bias 少於 0.5，就代表這硬幣傾向擲出反面，反之亦然。
猜完之後，我們就開始收集數據。我們會擲一次、兩次、三次、四次…… 我們可以擲很多很多次，把所有的正面和反面出現的次數寫下來，直到我們認為足夠為止。最理想的當然是無窮無盡不停地擲下去，但明顯這是不可能的，因為我們沒有無限的時間。就讓我們停止在第 N 次吧！
如果我們把「在開始實驗之前假設擲出正面的機率大概是一個峰值位於 0.5 的分佈，而我們知道擲出的結果不是正就是反」叫做資訊 I，我們就可以計算出在 I 情況下根據 N 次擲出的結果 {data} 所得出的傾向擲出正面機率 prob( head bias | {data}, I )。因為我很懶不想自己用手擲，下圖就是我用電腦模擬的計算結果：
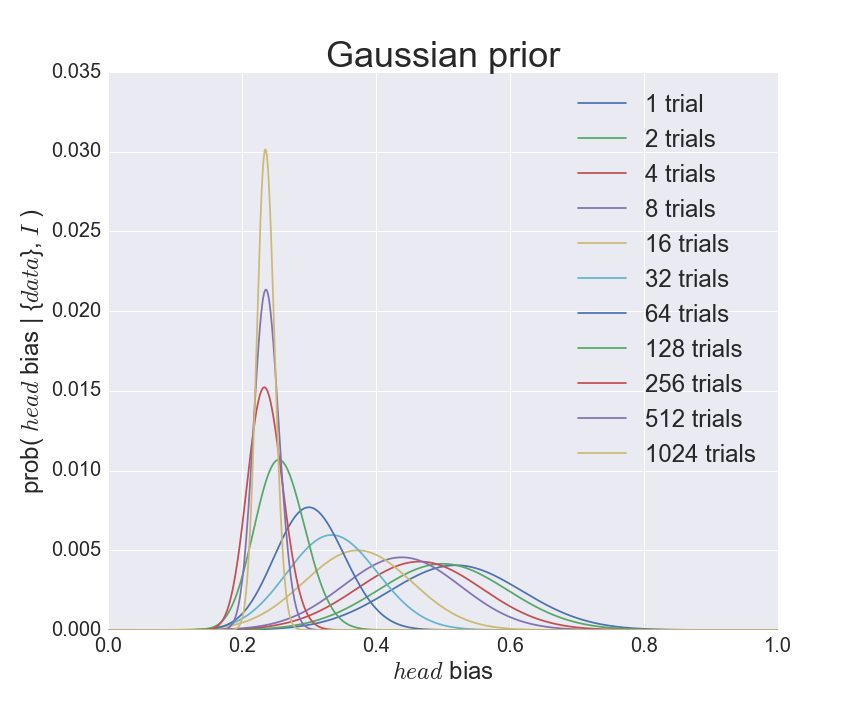使用電腦模擬擲一個不公平的硬幣。前設是一個平均值為 0.5 的高斯分佈。
縱軸是傾向擲出正面的機率、橫軸是擲出正面的傾向，不同顏色代表由 1 次到 1024 次不同的拋擲次數 N。我們可以看到，機率的峰值由很少拋擲次數 (N = 1, 2, 4, 8 trials) 時位於 0.5 附近，到擲了很多次之後 (N = 128, 256, 512, 1024) 移到 0.25 附近。而且，這個分佈的形狀亦由很闊變得越來越窄。為什麼呢？其實很簡單，因為我預先設定了這硬幣是不公平的，head bias = 0.25。換句話說，我預設了此硬幣傾向擲出反面多於正面，比例是每三次反面只有一次正面。在 N 很小時，我們數據不足、不能確定這個硬幣的傾向，因此分佈的形狀很闊。當 N 越來越大，即我們擁有的數據越來越多，我們就能比較肯定這個硬幣的傾向，分佈的形狀就變窄了。
神探伽利略也有過這一段，湯川學說明為什麼只憑猜測和直覺很容易會犯錯。
這就是一個最簡單的數據分析示範。也是為什麼費曼說我們要去分析事情發生的可能性，而不要只是說「有可能」或「不可能」。由此例子我們可以清楚的看到，只根據很少的數據去猜測，很可能會得出錯誤的結論。
我們也可以對另一個假設重複以上分析 (當然是用電腦模擬，不然擲到手斷也擲不完一千次……)，即在非常無知，0 <= prob( head bias | I ) <= 1 的前設下，看看結果會有什麼分別：
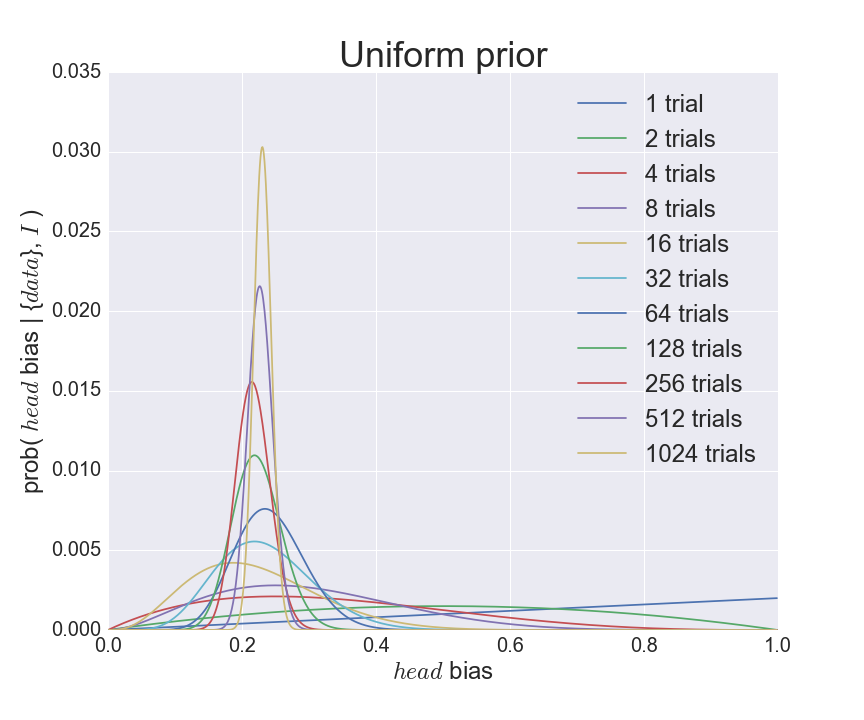同樣的電腦模擬，不過前設為一個由 0 到 1 的均等分佈。
與我們預期一樣，在擲了一千多次之後，計算結果已經非常接近預設的 0.25。值得留意的是在N很小的時候，分佈的闊度比上面的分析闊非常多。這很合理，因為我們假設了一個均等的前設！我們可以看到，在對一個理論非常無知的情況下，數據是非常非常重要的。如果我們只有寥寥可數的幾個數據，就要謹記我們的誤差會非常之大。例如我們常聽到人說「我幾個朋友都有 xxx 的情況」，我們就應該份外留心，這些結論的不確定性會非常之大。反之，如果我們知道一個理論的背後有著非常大量的數據支持，例如經過廣泛科學界、很多科學家驗證過的理論，我們就有理由相信這些結果的不確定性會很小。這就是科學精神，是理性、客觀的分析。
費曼在一次物理演講時說：「如果你想知道大自然如何運作，我們就要小心地觀察。它看起來如何運作就是如何運作。你不喜歡嗎？去其他地方吧，去其他擁有比較簡單的物理定律、哲學上比較令人愉快、心理學上比較容易的宇宙吧。我無能為力，OK？」
There’s a kind of saying that you don’t understand its meaning, ‘I don’t believe it. It’s too crazy. I’m not going to accept it.’… You’ll have to accept it. It’s the way nature works. If you want to know how nature works, we looked at it, carefully. Looking at it, that’s the way it looks. You don’t like it? Go somewhere else, to another universe where the rules are simpler, philosophically more pleasing, more psychologically easy. I can’t help it, okay? If I’m going to tell you honestly what the world looks like to the human beings who have struggled as hard as they can to understand it, I can only tell you what it looks like.
費曼一生都堅守科學精神的第一原則：誠實。面對我們喜歡的結論時，我們要誠實地去提醒自己，結論雖然正面，仍有著一定的不確定性。我們必須考慮所有數據準確地計算出誤差的大小；面對我們不喜歡的結論時，我們更加要時刻警覺，不可以故意忽略某些數據去令結論變得比較滿意。欺騙他人很容易，但這代表我們同時欺騙了自己。
For a successful technology, reality must take precedence over public relations, for Nature cannot be fooled.
No comments:
Post a Comment